INTRODUCTION OF ISOMETRIC DRAWING
An Isometric Drawing is such a drawing that even a common man without any technical knowledge can understand very easily the size and shape of a component. This is also called a Three-dimensional drawing because in an Isometric Drawing there are three mutually perpendicular axes ( plural form of 'axis' ) that meet at a common point and also make an angle of 120° with each other. In the following picture provided, assume three axes named X, Y, and Z make a 120° angle with each other and meet at a point 'O'.
Isometric Drawing |
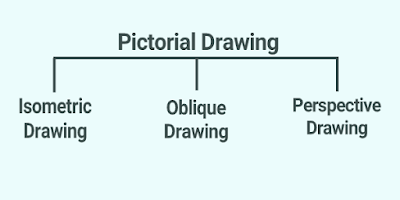
Actually, Isometric Drawing is a type of Pictorial Drawing. A pictorial drawing can be classified into three groups.....
1) Isometric Drawing
2) Oblique Drawing
3) Perspective Drawing.
Classification of Pictorial Drawing |
In some places, Orthographic Drawing is also added as a sub-category of Pictorial Drawing but this is not true as Orthographic Drawing is a kind of Layout Drawing. In the future, we will discuss in detail the differences between Pictorial Drawing and Layout Drawing.
However, out of the above-mentioned three sub-categories of Pictorial Drawing, Isometric Drawing, and Oblique Drawing have very much application in machine shop and metal working departments group whereas Perspective Drawing has a huge application in the civil engineering group of branches.
WHAT IS ISOMETRIC DRAWING
It is a technical method of visual or pictorial representation of three-dimensional objects for use in the field of engineering.
In an Isometric Drawing, the object makes an angle of 30° with the horizontal plane. Whereas it makes angles 60° & 120° with its plane of projections. For why the three coordinate axes come to meet at a single point and the angle between any two of them is 120° (degrees), thus sometimes it is also called an Axonometric Drawing.
In an Isometric drawing, all dimensions are drawn at full scale or any other scale ratio concerning the true dimensions of the component. These true dimensions can be obtained from either drawings completed in orthography or by measuring the object.
HOW TO START TO DRAW AN ISOMETRIC DRAWING
To start an Isometric Drawing of any kind of object, first of all, we should have to consider that the object must have its length, width, and height or the object has its three-dimensional axes.
Let us assume a 'cube' which we need to draw its isometric drawing.
Step 1: First of all, we need to draw three lines ( which would represent the three mutually perpendicular edges of that cube ) in such a manner that all three lines would come to meet a single point ( assume point 'A' ) and this 'A' point is resting upon horizontal line or horizontal plane. Moreover, two lines of those three lines, make an angle of 30° with the horizontal plane and the other line makes an angle of 90° with the horizontal plane or vertical with the horizontal plane, as shown in the following image.
HOW TO START TO DRAW AN ISOMETRIC DRAWING |
Step 2: After drawing two 30° lines and one vertical line, with the help of set-squares, BD and CF need to be drawn parallel to vertical line AE which would represent the height of the cube. Join DE and EF as shown in the following image.
HOW TO START TO DRAW AN ISOMETRIC DRAWING |
Step 3: Draw a parallel line of AB from point F and draw a parallel line of AC from point D, with the help of set-squares. DG and FG meet at a point G, as shown in the following image.
OR
Take AB as the radius with your compass and make arcs from centering the pointer of your compass on points D and F respectively. Both arcs cut a point on G Join DG and FG. That's it!
ISOMETRIC DRAWING |
ISOMETRIC AXES
In Isometric Drawing, those basic three lines that represent the three mutually perpendicular edges of any object are called jointly the Isometric Axes. Individually they are called the Isometric Axis.
Isometric Axes |
Generally, at the time of drawing an isometric drawing of any object, those axes are kept in front position but it solely depends upon the geometrical shape of the object.
ISOMETRIC LINES AND NON-ISOMETRIC LINES
In an isometric drawing, such lines that are parallel to any of the isometric axes are called Isometric Lines and those lines that are not parallel to any isometric axis are called Non-Isometric Lines.
ISOMETRIC DRAWING |
The above isometric drawing shows an image of a 'V-block'. In that isometric drawing, all the lines except FD and GD, are parallel to any axis of isometric axes. So, in the above isometric drawing, AB, AC, BL, AE, CH, EF, GH, IJ, and KL are the Isometric lines. Whereas FD, GD, and their parallel lines also are Non-isometric lines.
The length of Non-isometric lines of any object will not depend upon the scale ratio used to draw for isometric lines though non-isometric lines are drawn with the help of its adjacent isometric lines. Generally, non-isometric lines are always used to draw the slant faces or planes of the object, and moreover, the object is resting at an angle of 30° with the horizontal plane in the isometric drawing. For these reasons, non-isometric lines are drawn at the very least by locating their starting point and end point from their adjacent isometric lines. To locate of endpoints of non-isometric lines with the help of adjacent isometric lines, there are two methods have been deployed. Those are...
1) Off-set method and
2) Box method.
OFFSET METHOD IN ISOMETRIC DRAWING
As the name indicates the procedures of this method. This method is very much suitable for those objects that consist of many numbers of slant faces or planes at many numbers of different angles.
BOX METHOD IN ISOMETRIC DRAWING
In this method, the object is assumed to be inside a square, parallelogram, or rectangular box. The box structure depends upon the size and shape of the component. The starting points and end points of these non-isometric lines are located and by joining these points an isometric view is obtained.
We will see and learn about these steps more briefly at the time of application of Isometric drawing of various types of objects later.
ANGLES IN ISOMETRIC DRAWING
As said earlier, in an Isometric Drawing, the object makes an angle of 30° with the horizontal plane. Whereas it makes angles 60° & 120° with its plane of projections. The actual angles of surfaces of any object will not have the value in the isometric drawing and because of this reason, angles in the isometric drawing are also termed as Isometric Angles. The isometric angle value will be more in some cases and will be less in other cases than its actual or true value of inclination.
For example, in the isometric view of a prism shown below, the actual or true value of all angles of surfaces is 90°. But in isometric drawing the angles are 60° and 120°.
ANGLES IN ISOMETRIC DRAWING OF A PRISM |
CIRCLES, SQUARES, AND RECTANGLES IN ISOMETRIC DRAWING
As the term indicates, the true shape of circles, squares, and rectangles will also be changed in an isometric drawing and these are termed Isometric Circles, Isometric Squares, and Isometric Rectangles respectively. The figure shown below is an example of these.
Circles and Squares in Isometric Drawing |
As shown in the figure above, the true shape of a circle will be Elliptical in shape after a change in an isometric drawing and it is termed an Isometric Circle. Just like a circle, the true shape of a square and a rectangle will be Rhombus and Parallelogram respectively in shape after change in an isometric drawing and these are termed as an Isometric Square and Isometric Rectangle as described above.
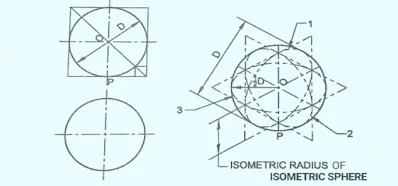
SPHERES IN ISOMETRIC DRAWING
The actual or true shape of a Sphere which can be seen in an orthographic view is a complete circle of equal radius from any direction and it is equal to the radius of the sphere. Hence, the shape of a sphere in an isometric drawing is also a circle of the same diameter as the sphere in true shape and it is termed an Isometric Sphere as shown in the figure below.
SPHERES IN ISOMETRIC DRAWING |