Post Summarization:
What is Conic?
Conic can be four (4) types:
 |
What is an Ellipse?
The meaning of ELLIPSE is flattened circle or oval. In general, in a pictorial drawing, a circle is represented by an ellipse. It has a less applications or is rarely used in engineering drawing or in engineering fields, however, this has a huge application in mathematics and adopted for better aesthetics.
Definition Of ELLIPSE
A closed curve is generated by the locus of a point, rotating in such a direction that the sum of its distances from two fixed points is always constant ratio (less than 1).
The fixed points are known as Foci (plural) and Focus (singular). The sum of distances from foci is equivalent to the length of the Major axis that is constant.
Examples of Ellipse
There are not too many practical examples of ellipses. However, Earth's orbit around the sun is in the shape of an ellipse, a race track shape is an example of an ellipse, the shape of elliptical gears is an example of an ellipse, etc.
Definition Of Parabola
A curve is generated by a locus of a point, rotating so that its distance from a fixed point is equal to its distance from a fixed line.
The fixed point is known as the Focus point and the Fixed line is known as the Directrix.
Definition Of Hyperbola
A special arch-shaped curve is generated by a locus of a point, rotating so that the distances from that point to a fixed point (the focus) and from that point to a fixed straight line (the directrix) are always in the same ratio (greater than 1).
Some Important Terms Or Elements Frequently Used In Ellipse, Parabola And Hyperbola:
Major Axis
The longest axis in an ellipse is termed a Major Axis which passes through the center at the right angle (90°) to the minor axis and perpendicular to the directrix.
Generally, the total length of the Major axis is not used in Parabola and hyperbola but it can be found by mathematical calculations.
Here, 'AB' is the major axis (see the below image).
Minor Axis
The maximum length that bisects the major axis at the right angle (90°) and parallel to the directrix is termed the Minor Axis.
Generally, the total length of the Minor axis is not used in Parabola and hyperbola but it can be found by mathematical calculations.
Here, 'CD' is the minor axis (see the below figure).
Directrix
The imaginary line which is perpendicular to the major axis and parallel to the minor axis is termed a Directrix.
It is an imaginary line that isn't physically present (in an ellipse, parabola, or hyperbola) but it involves directly constructing an ellipse, parabola, and hyperbola and calculating its mathematical deductions.
Here, 'DD1' is the directrix (see image).
Vertex
The endpoints of the major axis on the curve are termed Vertex or Vertex Points. Here 'A' and 'B' are the vertex points.
Vertex is commonly used to draw an ellipse, parabola, and hyperbola.
Co-Vertex
The endpoints of the minor axis on the curve are called Co-Vertex or Co-Vertex Points. Here 'C' and 'D' are the co-vertex points.
Generally, co-vertex can be found in only ellipse, and not in parabolas and hyperbolas.
Focus (Plural - Foci)
When an arc is drawn, taking 'C' or 'D' as a center point and with the radius equal to half of the major axis (i.e. AB/2) in such a way that it would cut the major axis on 'F1' and 'F2' respectively then 'F1' and 'F2' are termed individually as Focus or collaboratively Foci (Plural) or Focal Points.
Focus is commonly used to draw an ellipse, parabola, and hyperbola.
Focal Radii
The distances from any point (say 'P') on the curve to the focal points 'F1' and 'F2' are called Focal Radii or individual Focal Radius.
The sum of the Focal Radii is always constant and equal to the length of the Major Axis.
∴ PF1 + PF2 = Major Axis (AB) = Constant.
Generally, Focal Radii can be found in ellipses, and not in parabolas and hyperbolas.
Focus Angle
The angle generated between two focal radii on any point (say 'P') on the curve is termed as Focus Angle or Focal Angle. Here, angle F1PF2 is the focus angle.
Generally, Focus Angle can be found in ellipse, not in parabola and hyperbola.
Eccentricity (e)
The ratio between the distances from the vertex to the focus and the vertex to the directrix is termed Eccentricity.
It can also be stated as the ratio of the distances from focus to any point (say 'P1') on the curve and the perpendicular distance of point 'P1' to directrix. Eccentricity is denoted by 'e'.
Eccentricity has a common use for drawing an ellipse, parabola, and hyperbola. However, the value of eccentricity changes accordingly for ellipse, parabola, and hyperbola.
Eccentricity is constant and it is always less than one (1) in ellipse.
∴ AF1/AO = Constant < 1
Or, P1F1/P1M = Constant < 1
Eccentricity is always Equal to one (1) in Parabola.
Eccentricity is constant and it is always greater than one (1) in Hyperbola.
Tangent And Normal To An Ellipse
In an ellipse, the line that bisects the focus angle or bisector of the focus angle (angle F1PF2) is termed Normal. Here, PN1 is Normal (See the above image).
The straight line that just touches the curve on any point (say 'P') but does not intersect the ellipse by any means and creates a 90° angle with the normal is termed a Tangent. Here, 'TT1' is a tangent (See the above image).
Generally, Normal can be found in ellipse, not in parabola and hyperbola, practically. And so the tangent also. However, sometimes we draw tangent-normal on Parabola and Hyperbola for simplicity.
How to Draw Tangent and Normal on an Ellipse (See Fig.)
Let's assume a point 'P' on an Ellipse, on which we need to draw a Tangent and Normal. Now follow these steps:
(1) Join point 'P' with the nearest focus point 'F' by a straight line.
(2) Draw a right (90˚) angle at point 'F' in such a way that the angle PFT is equal to 90˚ and 'FT' intersects the Directrix on point 'T'.
(3) Now, join point 'T' and point 'P' by a straight line to get the required Tangent of that Ellipse on the 'P' point.
(4) Online 'TP' and at the point 'P', draw another straight line at an angle of 90˚ to draw the Normal of that tangent. (See above image).
Methods To Draw Or Construct An Ellipse
There are various methods which can be used to draw an ellipse. However, some of them can't be commonly used to construct ellipses with any dimensions.
Following are the names of the methods to draw an ellipse:
(1) Concentric Circle Method.
(2) Arcs (Arcs of Circle) Method.
(3) Rectangle or Oblong Method.
(4) Parallelogram Method.
(5) Tangent Method.
(6) String and Pins Method or Loop Of The Thread Method.
(7) Paper Trammel Method.
(8) 4 Centre Method 'A' Type and 'B' Type.
(9) Eccentricity Method or General Method.
N.B. Eccentricity Method is a common method, that can be used to draw any ellipse, parabola, or hyperbola. However, this method is mainly used for drawing parabolas and hyperbolas.
(1) Concentric Circle Method
(i) Draw the major axis ‘AB’ (Say, 80 mm) and the minor axis ‘CD’ (Say, 60 mm) bisecting each other at a right angle at ‘O’.
(ii) Take center at ‘O’, and draw two circles with radius ‘OA’ and ‘OC’ respectively.
(iii) Now, divide the both major circle (Outer Circle) and minor circle (Inner Circle) simultaneously into twelve (12) equal divisions.
(iv) Now, mark the cut points on the major circle as a, b, c, d, e, f, g, and h. Similarly, mark the corresponding intersection points on the minor circle as ‘aʹ’, ‘bʹ’, ‘cʹ’, ‘dʹ’, ‘eʹ’, ‘fʹ’, ‘gʹ’, and ‘hʹ’. However, you can skip this step.
(v) Through points ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’, and ‘h’ on the outer circle, draw vertical parallel lines to the Minor axis with the help of sets-square taking a convenient length that it will cut those corresponding horizontal parallel lines from the inner circle. See ima ge.
(vi) Similarly, through points ‘aʹ’, ‘bʹ’, ‘cʹ’, ‘dʹ’, ‘eʹ’, ‘fʹ’, ‘gʹ’, and ‘hʹ’ on the inner circle, draw horizontal parallel lines to the Major axis taking a convenient length to intersect with the corresponding vertical parallel lines at points ‘P1’, ‘P2’, ‘P3’, ‘P4’, ‘P5’, ‘P6’, ‘P7’, and ‘P8’. See image.
(vii) Now join these all points through ‘A’, ‘P1’, ‘P2’, ‘C’, ‘P3’, ‘P4’, ‘B’,
‘P5’, ‘P6’, ‘D’, ‘P7’, and ‘P8’ with a smooth thick curve with the help of
French curves to complete the required ellipse.
(2) Arcs Method
(i) Draw a major axis ‘AB’ and a minor axis ‘CD’, bisecting each other at right angles at point ‘O’.
(ii) Now, take the center point as ‘C’ and a radius equal to half of ‘AB’ (i.e. ‘AO’) and draw arcs for cutting ‘AB’ at ‘F1’ and ‘F2’, the foci of the ellipse.
(iii) Take any convenient length and mark points 1, 2, 3, etc. on ‘AO’ as shown. See image.
(iv) Now, take a radius equal to ‘A to 1’ and draw arcs on both sides of ‘AB’ with centers‘ F1’ and ‘F2’ respectively.
(v) Now, take the radius as ‘B to 1’ and with the same centers ‘F1’ and ‘F2’, draw arcs intersecting the previous arcs at four points marked as ‘P1’.
(vi) Similarly, take a radius equal to ‘A to 2’ with the centers ‘F1’ and ‘F2’
respectively draw arcs on both sides of ‘AB’, and cut those four arcs with a
radius of ‘B to 2’ from centers ‘F1’ and ‘F2’ respectively and mark as ‘P2’.
(vii) Repeat that process again, draw arcs with radius ‘A to 3’ and ‘B to 3’ with the same centers as ‘F1’ and ‘F2’ to get the four cut points and mark ‘P3’ on them.
(vii) Now, draw a smooth thick curve through these points and complete the required ellipse. See image.
(3) Rectangle or Oblong Method
(i) First, draw the two axes ‘AB’ and ‘CD’ bisecting each other at ‘O’.
(ii) Now, construct a rectangle or oblong ‘EFGH’ having its length equal to the Major axis and breadth equal to the Minor axis.
(iii) Divide the ‘AO’
(Semi Major Axis) into a number of equal parts, say 4, and ‘AE’ into the same (4) numbers of equal
parts, numbering them from ‘A’ as
shown in the image.
(iv) Now, draw straight lines to join 1', 2', and 3' with point C.
(v) Now, from point ‘D’, draw lines through 1, 2, and 3 intersecting C1', C2', and C3' at points P1, P2, and P3 respectively. These points P1, P2, and P3 will create the one-quarter of the ellipse.
(vi) Repeat the same process to find out points ‘P4’, ‘P5’, ‘P6’, ‘P7’, ‘P8’, ‘P9’, ‘P10’, ‘P11’, and ‘P12’ in the remaining three-quarters of the ellipse. (See above image).
(vii) Now, with the help of French curves, draw a smooth and thick curve through points ‘A’, ‘P4’, ‘P5’, ‘P6’, ‘C’, ‘P7’, ‘P8’, ‘P9’, ‘D’, ‘P10’, ‘P11’, ‘P12’, and ‘A’ to complete the required ellipse. See image.
(4) Parallelogram Method
(i) With given internal angles, construct a parallelogram ‘EFGH’ having its length equal to the Major axis and breadth equal to the Minor axis.
(ii) Now, draw the two axes ‘AB’ and ‘CD’ intersecting each other at ‘O’.
(iii) Divide the ‘AO’
(Semi Major Axis) into a number of equal parts, say 4, and ‘AE’ into the same number of equal
parts, numbering them from ‘A’ as
shown in the image.
(iv) Now, draw straight lines to join 1', 2', and 3' with point C.
(v) Now, from point ‘D’, draw lines through 1, 2, and 3 intersecting C1', C2', and C3' at points R1, R2, and R3 respectively. R1, R2, and R3 points will create the one-quarter of the ellipse.
(vi) Repeat the same process to complete the remaining three-quarters of the ellipse (See above Fig.).
(vii) Now, with those points A, R1, R2, R3, C,..... as shown in the above image, draw a smooth and thick curve to complete the required ellipse in the Parallelogram method.
(5) Tangent Method
(i) First, draw the two axes ‘AB’ and ‘CD’ bisecting each other at ‘O’.
(ii) Now, construct a rectangle ‘EFGH’ having its length equal to the Major axis and breadth equal to the Minor axis.
(iii) Now, divide AE, EC, CF, FB, BG, GD, DH, and HA into the same number of equal parts, say 4, and mark them as a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, and x. See the below image.
(iv) Join ad, be, cf for one-quarter of ellipse.
(v) Similarly, complete the remaining three quarters of the ellipse by joining gj, hk, il, mp, nq, or, sv, tw, and ux.
(vi) Now, consider these all lines as tangents and draw a smooth-thick curve just by touching those tangents and completing the required ellipse. See the above image.
(6) String and Pins Method or Loop Of The Thread Method
(i) Draw the two axes ‘AB’ and ‘CD’ bisecting at ‘O’.
(ii) Take radius equal to ‘AO’(half of Major axis) and
center as ‘C’, draw arcs to cut on Major axis to locate the foci ‘F1’ and ‘F2’.
(iii) Insert a pin at each focus point and tie a piece of thread in the form of a loop around the pins, in such a way that the pencil point 'P' when placed in the loop (keeping the thread tight), is just on the endpoint ‘C’ of the Minor axis.
(iv) Similarly, move the pencil around the foci, maintaining an even tightness in the thread all around, and obtain the ellipse.
It is the evident of PF1
+ PF2 = CF1 + CF2
(7) Paper Trammel Method
(i) Draw the two axes ‘AB’ and ‘CD’ bisecting each other at point ‘O’.
(ii) Now, take two paper strips that may be used as a trammel, mark ‘PQ’ equal to half the minor axis and ‘PR’ equal to half the major axis. See image.
(iii) Place those paper strips so that ‘R’ can move vertically along the minor axis ‘CD’ and ‘Q’ can move horizontally along the major axis ’AB’. So, ‘P’ will be pointing to the required ellipse.
(iv) Now, start to move those paper strips to new positions as a trammel moves on, always keeping point ‘R’ on ‘CD’ (minor axis) and point ‘Q’ on ‘AB’ (major axis), obtain other points.
(v) Now, join those points with French curves and draw a smooth and thick curve to complete the required ellipse through these points.
See a Trammel Work (Demo)!
(8) 4 Centre Method 'A-Type'
A - Type
Draw an ellipse with a Major axis of 80 mm and a Minor axis of 60 mm.
(i) Draw a Major axis A1A2 equal to 80 mm and B1B2 equal to 60 mm, bisecting each other at a right angle (90˚) at point ‘O’.
(ii) Join A1B1 with a straight line and set off B1B3 equal to a-b= 10 mm (where, a= Semi Major Axis= ‘OA1’= 40 mm, and b= Semi Minor Axis= ‘OB1’= 30 mm.).
(iii) Draw a perpendicular bisector ‘P1’ on A1B3 which intersects ‘A1O’ at ‘M1’ and ‘B2O’ at ‘M2’.
(iv) Now, take ‘OM1’ distance and cut ‘M3’ from point ‘O’ on ‘OA2’.
(v) Similarly, take ‘OM2’ distance and cut ‘M4’ from point ‘O’ on ‘OB1’.
(vi) Join ‘M2’ and ‘M3’ and extend it up to a convenient length towards ‘P2’. See image.
(vii) Now, join ‘M4’ with ‘M3’ and ‘M4’ with ‘M1’ and extend those upto a convenient length towards ‘P4’ and ‘P3’ respectively.
(viii) Take ‘A1M1’ as radius and ‘M1’ as center, draw arc ‘P1AP3’ and take ‘A2M3’ as radius and ‘M3’ as center draw arc ‘P2A2P4’.
(ix) Similarly, take ‘B1M2’ as the radius and ‘M2’ as a center, draw arc ‘P1B1P2’, and take ‘B2M4’ as the radius and ‘M4’ as the center draw arc ‘P3B2P4’ to complete the required ellipse.
B - Type
Draw an ellipse with a Major axis of 80 mm and a Minor axis of 40 mm.
(i) Draw Major Axis ‘AB’ equal to 80 mm and Minor Axis ‘CD’ equal to 40 mm, bisecting each other at a right angle (90˚).
(ii) Enclose both axes within a rectangle ‘EFGH’ of 80 mm length and 40 mm width, see image.
(iii) Join ‘CE’, ‘CH’, ‘DF’, and ‘DG’ with a straight line.
(iv) Bisect ‘AE’ to find out its middle point marked as ‘P’.
(v) Join ‘PD’ by a straight line that intersects EC at point ‘K’.
(vi) Now, draw a perpendicular bisector of ‘KD’ to a convenient length that will intersect the extended DC at point ‘S’. See figure.
(vii) Again join ‘AK’ by a straight line, and draw a perpendicular bisector on it to intersect the major axis ‘AB’ at point ‘f1’.
(viii) Similarly, get points ‘R’ and ‘f2’. Or take the distance ‘SC’ as the radius and take point ‘D’ as a center and cut on the extended ‘CD’ to get the point ‘R’. For getting the ‘f2’ point, take ‘Af1’ as the radius and take the point ‘B’ as a center and cut on the major axis. Now, ‘f1’, ‘f2’, ‘S’, and ‘R’ are the four points to draw the ellipse.
(ix) Now, take center as ‘f1’ and ‘f2’ and draw arcs KAK' and MBM' respectively.
(x) Similarly, take center as ‘R’ and ‘S’ and draw arcs K'CM' and MDK respectively to complete that required ellipse.
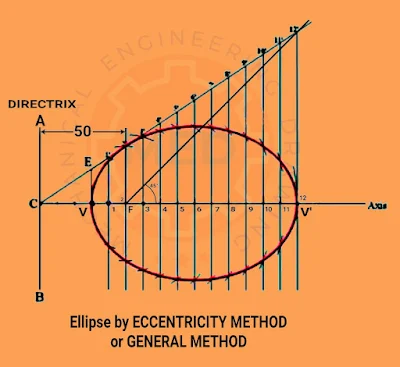
(9) Eccentricity Method or General Method
Draw an ellipse with the distance of the focus from the Directrix is equal to 50 mm and eccentricity is equal to 2/3
(i) Draw any vertical line AB as directrix.
(ii) take a point ‘C’ on the directrix and draw the major axis perpendicular to the AB (directrix).
(iii) Mark a focus F on the axis such that CF = 50 mm.
(iv) Divide CF into 5 equal divisions (sum of numerator and denominator of the eccentricity.).
(v) Mark the vertex point as ‘V’ on the third division point from point C.
Thus, VF = 2, and VC = 3, as eccentricity (e) = 2/3 (Given).
(vi) At vertex ‘V’, draw a perpendicular VE equal to VF.
(vii) Draw a straight line joining C and E, and extend this line to a convenient length. See Above Fig.
(viii) At focus point 'F', draw a line at 45˚, which will intersect 'CE' at point 12'. From 12', draw a perpendicular on the major axis at point 12. See Fig.
(ix) Now, 'V' to 12 is the total length of the major axis.
(x) Mark points 1, 2, 3, etc on the major axis, and through these, draw perpendiculars to intersect CE at 1', 2', 3', etc respectively. See image.
(xi) Now, take the center as point F and radius equal to 1-1', and draw arcs to intersect the perpendicular 1-1' on both sides.
(xii) Again, take the center as F on the major axis and radius 2-2', and draw arcs to intersect the perpendicular 2-2' on both sides.
(xiii) Similarly, take radius 3-3' and 'F' as a center, cut on both sides of the 3-3' perpendicular line, and in the same way, get the remaining cut points on those remaining perpendicular lines.
(xiv) Now, with the help of French curves draw the required ellipse through these points.
The eccentricity method is also used for drawing a Parabola, and Hyperbola in the same way as described above. Thus, it's also known as General Method or Common Method.