POLYGON

Post Summarization:

● What is Polygon - Introduction.

● Types of Polygon.

● Methods to draw Regular Polygons. (In this chapter we'll see the methods to draw a Regular Polygon only as in Engineering Drawing mostly a Regular Polygon is used Practically.) - UPDATED

WHAT IS POLYGON: INTRODUCTION

A plain area, surrounded by multiple sides (more than two sides or minimum by three sides!) is called a Polygon.

A Polygon is named according to its total number of sides as follows.

Sides Three (3 Nos.) Four (4 Nos.) Five (5 Nos.) Six (6 Nos.) Seven (7 Nos.) Eight (8 Nos.) Nine (9 Nos.) Ten (10 Nos.) Eleven (11 Nos.) Twelve (12 Nos.)

Termed As Triangle Quadrilateral Pentagon Hexagon Heptagon Octagon Nonagon Decagon Undecagon Duodecagon

The sum of the internal angles of any polygon can be found by an equation:

   {2(n-2)}×90°

= (2n-4)×90°

(Where, n = Number of sides of Polygon)

From the above equation, if we put the value of n = 3 and n = 4; we'll get the sum of the internal angles of a triangle is 180° and the sum of the internal angles of a Quadrilateral is 360°.

As, triangles and quadrilaterals also follow that above equation as like other polygons, thus, a triangle or a quadrilateral is also a Polygon.

The total number of Diagonals in a Polygon can be found by an equation:

n(n-3)/2

(Where, n = Number of sides of Polygon)

From the above equation, if we put the value of n=11, then the total number of Diagonals in an Undecagon would be 44.

Types Of Polygon:

Polygon can be classified into two types.

1) Regular Polygon.

2) Irregular Polygon.

Regular Polygon:

A Polygon having sides with equal lengths is called a Regular Polygon. 

In geometry, it's saying, that when every side is equal then its opposite angles are also equal.

Thus, as shown in the above Regular Pentagon, each internal angle would be 108° when all sides of the Pentagon are the same in length (here, it's 25 mm).

From the equation of "sum of internal angles of a Polygon", we know...

(2n-4)×90°       

[ Putting the value of n=5 ] we get,

{(2×5)-4}×90°

=540°

Therefore, the total or sum of all the internal angles in a Polygon is equal to 540°. When we divide this with a total number of internal angles (here it's 5), we get...

(540°÷5) = 108°

Thus, each internal angle would be 108° if every internal angle is the same. And if every internal angle is the same then its opposite sides are also equal, that's a Regular Polygon.

Irregular Polygon:

When a Polygon, has sides of unequal length and thus its internal angles are also not equal, is called an Irregular Polygon.

In the above image, we can see a Polygon with 8 unequal sides (An irregular Octagon). Thus, its internal angles are also not equal.

Methods to Draw Regular Polygons:

There are many approved methods available for Drawing a Regular Polygon and they are classified as Common Methods and Special Purpose Methods. Here, we'll discuss the all-important methods that are generally used practically in industries or in schools and colleges. 

Common Methods

These methods are vastly used in schools, colleges, and industries. As there is a fixed process to draw regular polygons of any number of sides so, it’s easy to apply for all kinds of regular polygons. The Perpendicular Bisector method, Polygon in a Circle method, Angular method, and Semi Circular Method fall under Common Methods.

 

 

1. Perpendicular Bisector Method

 

This method can be utilized to draw a regular polygon with any number of sides, thus it is a common method.

 

Draw a regular Heptagon with Perpendicular Bisector Method:

 Assume the sides of a Regular Heptagon (7 sides) to any convenient length, say ‘AB’ in this case.

 

Perpendicular Bisector Method ‘A-TYPE’: Method (Process): 

(i) Take ‘AB’ horizontally as a diameter, and draw a Perpendicular Bisector that divides equally the ‘AB’ line into two parts. Now, take the middle point of the 'AB’ line as the center of a circle, and describe a Semi-circle or Arc, that will cut the Perpendicular Bisector at a point. Give a name ‘4’ to that cutting point.

 

(ii) Now, with either A or B as the center, and the total length of  ‘AB’  as the radius, draw another arc that will cut the Perpendicular Bisector at a point on the same side of that semi-circle or previous arc. Give a name ‘6’ to that cut point.

 

(iii) Again draw a perpendicular bisector to equally divide the length of ‘4 to 6’, and mark the middle point as ‘5’ in between ‘4 and 6’.

(iv) Now, take the length of ‘4 to 5’ or ‘5 to 6’ on the compass, and from point ‘6’ start to inscribe with that fixed length to Obtain point ‘7’. Similarly 3, 8, 9, 10, 11, 12, etc as per the requirement.

 

(v) For a Heptagon, take point ‘7’ as a center, and take ‘7 to A’ or ‘7 to B’ as the radius, and draw a Circle.

(The center point of the circle varies according to the number of sides of the polygon and the Radius is calculated from that point to ‘A’ or ‘B’. It means, for a triangle - point ‘3’, for a square - point ‘4’, and for a Pentagon - point ‘5’ should be taken as the center of the circle. The radius of the circle also changes in the same way, for Triangle-‘3 to A’ or ‘3 to B’, for Square-‘4 to A’ or ‘4 to B’, for Pentagon-‘5 to A’ or ‘5 to B’, and so on!)

               

(vi) Now, take the whole ‘AB’ length on the compass, and start to cut from point ‘A or B’ on the circumference of that circle. Give names to those cut points as C, D, E, F, and G respectively. See the image.

 

(vii) At last, join BC, CD, DE, EF, FG, and GA with straight lines, and complete the required Heptagon.

 

The following image shows a square, a regular pentagon, a regular hexagon, and a regular Octagon simultaneously, all polygons are constructed with AB length as a fixed or common length of sides.

 

 

 

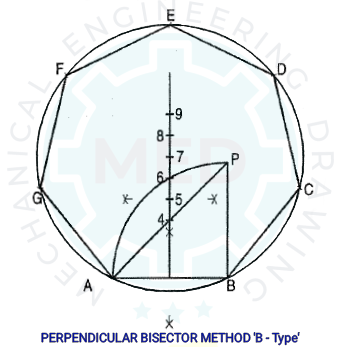
Perpendicular Bisector Method ‘B-TYPE’: Method (Process):

 

(i) Take ‘AB’ horizontally as a diameter, and draw a Perpendicular Bisector that divides equally the ‘AB’ line into two parts.

 

(ii) Now, take the length of the “AB’ line and draw an Isosceles triangle that has a 90˚ angle too, as shown in the image, The Hypotenous of that triangle cuts the Perpendicular Bisector of ‘AB’ at point ‘4’.

 

(iii) Now, with either A or B as a center, and take again the total length of  ‘AB’  as the radius, draw an arc that will cut the Perpendicular Bisector at a point on the same side of that semi-circle or previous arc. Give a name ‘6’ to that cut point.

 

(iv) Again draw a perpendicular bisector to equally divide the length of ‘4 to 6’, and mark the middle point as ‘5’ in between ‘4 and 6’.

 

(v) Now, take the length of ‘4 to 5’ or ‘5 to 6’ on the compass, and from point ‘6’ start to inscribe with that fixed length to Obtain point ‘7’. Similarly 3, 8, 9, 10, 11, 12, etc as per the requirement.

 

(vi) For a Heptagon, take point ‘7’ as a center, and take ‘7 to A’ or ‘7 to B’ as the radius, and draw a Circle.

(The center point of the circle varies according to the number of sides of the polygon and the Radius is calculated from that point to ‘A’ or ‘B’. It means, for a Triangle - point ‘3’, for a Square - point ‘4’, for a Pentagon - point ‘5’ should be taken as the center of the circle. The radius of the circle also changes in the same way, for Triangle-‘3 to A’ or ‘3 to B’, for Square-‘4 to A’ or ‘4 to B’, for Pentagon-‘5 to A’ or ‘5 to B’, and so on!)

 

(vii) Now, take the whole ‘AB’ length on the compass, and start to cut from point ‘A or B’ on the circumference of that circle. Give names to those cut points as C, D, E, F, and G respectively. See the image.

 

(viii) At last, join BC, CD, DE, EF, FG, and GA with straight lines, and complete the drawing by leveling the dimensions on it.

 

 

 

2. Polygon in a Circle Method

 

It’s a common method, that can be utilized to draw a regular polygon with any number of sides.

 

Construct a regular Pentagon by “In a Circle Method”:

 Assume the diameter of the circle is only given as ‘AB’ and a Regular Pentagon (5 sides) needs to be drawn.

 

Method (Process):

(i) Draw a given diameter, say ‘AB’ in this case, and mark its middle point as ‘O’.

 

(ii) Now, divide ‘AB’ into five equal parts (the same number of parts as the number of sides of the Polygon as given a ‘Pentagon’) and number them as shown in the image.

 

(iii) With centers ‘A’ and ‘B’, and take the radius as ‘AB’, draw arcs intersecting each other at point ‘P’.

 

(iv) Draw a straight line to join ‘P’ and ‘2’, and extend it to meet the circumference of the circle at point ‘C’. Now ‘AC’ is the length of the side of the regular pentagon. (Remember, in this method, joining ‘P’ and ‘2’ is mandatory for getting the length of sides of a regular polygon with any number of sides.)

 

(v) Starting from point ‘C’ on the circumference, step-off on the circle, divisions ‘CD’, ‘DE’, ‘EF’, and ‘FA’ equal to ‘AC’.

 

(vi) At last, draw lines ‘CD’, ‘DE’ ‘EF’, and ‘FA’ to complete the regular Pentagon.

 

 

 

 

3. Semi Circular Method

 

This method also can be utilized to draw a regular polygon with any number of sides, thus it is a common method too. In this case, assume the sides of a Regular Heptagon (7 sides) to any convenient length, say ‘AB’.

 

 

Draw a Heptagon by semi-circular Method ‘A-TYPE':

 

Method (Process):

 (i) Draw a horizontal line equal to the given length ‘AB’, and extend it to a convenient length up to ‘P’.

 

(ii) Now, take point ‘A’ as a center, and with radius AB, draw a semi-circle ‘BP’.

 

(iii) With a protractor or divider, divide the semi-circle into seven equal parts (same as the

number of sides, in this case, a Heptagon). Number the division-points as 1, 2, 3, etc. starting from point ‘P’.

 

(iv) Draw a line for joining point ‘A’ with the second division-point ‘2’.

 

(v) Now, draw perpendicular bisectors on both ‘A2’ and ‘AB’, intersecting each other at ‘O’.

 

(vi) With center ‘O’ and radius ‘OA’ or ‘OB’, draw a circle.

 

(vii) Now, take the ‘AB’ length on the compass, and starting from ‘B’, cut the circumference of the circle (in an anti-clockwise direction) at points ‘C’, ‘D’, ‘E’, and ‘F’.

 

(viii) At last, join ‘BC’, ‘CD’, ‘DE’, ‘EF’, and ‘F2’ with straight lines to complete the required regular Heptagon.

 

 

 

Draw a Heptagon by Semi Circular Method ‘B-TYPE’:

 

Method (Process):

(i) Draw a horizontal line equal to the given length ‘AB’, and extend it to a convenient length up to ‘P’.

 

(ii) Now, take point ‘A’ as a center, and with radius AB, draw a semi-circle ‘BP’.

 

(iii) With a protractor or divider, divide the semi-circle into seven equal parts (same as the number of sides, in this case, a Heptagon). Number the division-points as 1, 2, 3, etc. starting from point ‘P’.

 

(iv) Draw a line for joining point ‘A’ with the second division-point ‘2’.

 

(v) Now, join ‘A3’, ‘A4’, ‘A5’, ‘A6’, and ‘AB’ with straight lines and extend up to a convenient length as shown in the image.

 

(vii) Now, take the ‘AB’ length on the compass, and starting from ‘B’, cut the extended lines (in an anti-clockwise direction) at points ‘C’, ‘D’, ‘E’, and ‘F’.

 

(viii) At last, join ‘BC’, ‘CD’, ‘DE’, ‘EF’, and ‘F2’ with straight lines to complete the required regular heptagon.

 

 

 

4. Angular Method

 

This method can be utilized to draw both a regular or irregular polygon with any number of sides, thus it is a common method too. In this method, polygons are drawn with the help of an Angle between two (2) adjacent sides. In this regard, a protractor is very helpful in measuring the angles confirmed.

                

Construct a Triangle by Angular Method:

 

Assume the sides of an Equilateral Triangle (3 sides equal) to any convenient length. Each internal angle is equal to 60˚ in the Equilateral Triangle. Therefore, the external angle is 120˚

                                                                   

We know the sum of internal angles  

 (2n-4)90˚                         where, n=3

                                                             

 = (2)90˚

                                                             

 = 180˚                           

thus, internal angle, (180˚/3) = 60˚ and external angle = (180˚-60˚)= 120˚

 

 

Method (Process):

(i) With center ‘O’, draw the circle with a given radius.

 

(ii) Now, draw a vertical radius ‘OA’ for dividing the circle into 3 parts. Here, in this case, it is an Equilateral Triangle, so each part would be of 120° angle.

 

(iii) Then, draw radii ‘OB’ and ‘OC’ with the help of a protractor, compass, or 30°-60° set-square, such that angle ˚AOB = ˚BOC = ˚AOC = 120°.

 

(iv) Now, from ’A’, ‘B’, and ‘C’, draw tangents to the circle, intersecting one another at the ‘E’, ‘F’, and ‘G’ points. Thus EFG is the required Equilateral Triangle.

 

 

Construct a Square by Angular Method:

Now, assume the sides of a Square (4 sides equal) to any convenient length. Each internal angle is equal to 90˚ in Square. Therefore, external angle = 180˚-90˚= 90˚

                                                                   

We know the sum of internal angles  

 (2n-4)90˚                         where, n=4

                                                             

 = (4)90˚

                                                             

 = 360˚                           

thus, internal angle, (360˚/4) = 90˚ and external angle = (180˚-90˚)= 90˚

 

Method (Process):

(i) With center ‘O’, project the circle with a given radius.

 

(ii) Draw diameters ‘AB’ and ‘CO’ at right angles to each other as shown in the image. It is a Square, for this reason, with the use of a protractor, compass, or sets-square, the circle should be divided into 4 equal parts so that each part would be of a 90° angle. 

 

(iii) At ‘A’, ‘B’, ‘C’, and ‘D’, draw tangents to a convenient length those intersecting at ‘E’, ‘F’, ‘G’, and ‘H’. So the EFGH is the required square.

 

 

 

Construct a Hexagon by Angular Method:

In this case, assume the sides of a regular Hexagon (6 sides equal) to any convenient length. Each internal angle is equal to 120˚ in Hexagon. Therefore, external angle = 180˚-120˚= 60˚

                                                                   

We know the sum of internal angles 

=  (2n-4)90˚                         where, n=6

                                         

= (8)90˚

                                                             

 = 720˚                           

thus, internal angle, (720˚/6) = 120˚ and external angle = (180˚-120˚)= 60˚ 

 

Method (Process): 

 

(i) With center ‘O’, project the circle with a given radius.

 

(ii) It is a Hexagon, for this reason, the circle should be divided into 6 parts so that each part would be of 60° angle. Draw diameters ‘AB’, ‘CD’, and ‘EF’ at 60˚ angle to each other as shown in the image.

 

(iii) At ‘A’, ‘B’, ‘C’, ‘D’, ‘E’, and ‘F’ draw tangents to a convenient length those intersecting each other at ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, and ‘6’. So the ‘123456’ is the required regular Hexagon. 

 

 

 

Construct an Octagon by Angular Method:

 

Again, assume the sides of a Regular Octagon (8 sides) to any convenient length. Each internal angle is equal to 135˚ in an Octagon. Therefore, external angle = 180˚-135˚= 45˚

                                                                   

We know the sum of internal angles   

(2n-4)90˚                         where, n=8

                                                             

= (16-4)90˚

                                                             

 = 1080˚                           

thus, internal angle, (1080˚/8) = 135˚ and external angle = (180˚-135˚)= 45˚

 

 

Method (Process):

(i) With center ‘O’, draw the circle diameters ‘AB’ and ‘CD’ perpendicular to each other and complete the circle.

 

(ii) Now, with the help of a protractor or compass, divide the circle into 8 parts (as here in this case, it is an Octagon), so that each part would be a 45° angle.

 

(iii) Draw tangents at the eight points ‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘F’, ‘G’, and ‘H’ intersecting one another at point ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, and ‘8’. Now, ‘12345678’ is the regular octagon.

 

 

 

 

Special Purpose Methods

 

These methods are rarely used for a special purpose only and unlike the above processes, there is no fixed process to draw regular polygons. The Arc method, Three-circle method, and Across-Flat method fall under Special Purpose Methods.

 

1. Arc Method

In the Arc Method, the construction of regular polygons is mainly done by drawing arcs, thus it is termed as Arc method.

 

Draw a regular Pentagon (5 sides) by Arc Method: 

 

Method (Process): 

(i) Assume a center point ‘O’, and draw the circle with a given radius.

 

(ii) Draw diameters ‘AB’ and ‘CD’ perpendicular to each other.

 

(iii) Bisect either ‘AO’, or ‘OB’ in a point P.

 

(iv) Now, take the center point as ‘P’ and radius as ‘PC’, and draw an arc cutting ‘OB’ at point ‘Q’.

 

(v) Now, take the center point as ‘C’, and with radius ‘CQ’, draw an arc cutting the circumference of the circle at points ‘E’ and ‘F’.

 

(vi) With the same ‘CQ’ radius, and taking center points as ‘E’ and ‘F’ respectively, again draw arcs cutting the circumference of the circle at the ‘G’ and ‘H’ points.

 

(vii) Now, draw straight lines to join ‘C’, ‘E’, ‘G’, ‘H’, and ‘F’, to complete the required regular pentagon.

 

 

 

Draw a regular Hexagon (6 sides) by Arc Method:

 

Method (Process):

(i) Draw a circle of radius as given 32 mm. (To draw a regular Hexagon In the Arc method, the length of the side is equal to the radius of the circle.)

 

(ii) Now, draw the diameter ‘AD’ as shown in the image.

 

(iii) Take point ‘A’ as a center and with the same given radius, draw an arc that cuts the circumference of the circle at ‘B’ and ‘F’ points.

 

(iv) Similarly, with the same given radius and taking the center point as ‘D’, draw another arc that cuts the circumference of the circle at ‘E’ and ‘C’ points.

 

(v) Now, join ‘AB’, ‘BC’, ‘CD’, ‘DE’, ‘EF’, and ‘FA’ with straight lines to complete the required regular Hexagon.

 

 

 

Draw a regular Hexagon (6 sides) by (Inscribing) Arc Method:

 

This method is done by only inscribing arcs on the circle circumference in a clockwise or anti-clockwise direction, thus this arc method is termed as Inscribing Arc Method, and this method is applicable for drawing regular Hexagon only but very quickly!

 

Method (Process):

(i) Draw a circle of radius as given 32 mm. (To draw a regular Hexagon In the Arc method, the length of the side is equal to the radius of the circle.)

 

(iii) Take the same given radius of 32 mm and take ‘B’ as starting point, and start to inscribe the circumference of the circle at ‘C’, ‘D’, ‘E’, and ‘F’ points.

 

(iv) Now, join ‘AB’, ‘BC’, ‘CD’, ‘DE’, ‘EF’, and ‘FA’ with straight lines to complete the required regular Hexagon.

  

 

 

Construct a regular Heptagon (7 sides) by Arc Method:

 

Method (Process):

(i) With centre ‘O’, draw the given circle.

(ii) Draw a diameter ‘AB’ on the circle. Thus, radius ‘AO’ is equal to radius ‘OB’ (Diameter = D = 2R).

(iii) Now, make a center point ‘A’ and radius ‘AO’, and draw an arc, cutting the circumference of the circle at points ‘E’ and ‘F’.

 

(iv) Join points ‘E’ and ‘F’ by drawing a straight line ‘EF’, cutting radius line ‘AO’ at point ‘G’.

 

(v) Now, either  ‘EG’, or ‘FG’ is the length of the side (as EG=FG) of the heptagon.

 

(vi) Therefore, take that ‘EG’ length on your compass and start to cut off divisions equal to ‘EG’, starting from point ‘A’ on the circumference of the circle, in an anti-clockwise direction. Naming those cutting points as ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, and ‘6’.

 

(vii) Now, join those division points (‘A1’, ‘12’, ‘23’, ‘34’, ‘45’, ‘56’, and ‘6A’) by straight lines and obtain the required regular Heptagon.

 

 

 

Draw a regular Octagon (8 sides) by Arc Method:

 

Method (Process): 

(i) Take center point ‘O’, and draw a circle with a given radius.

 

(ii) Draw diameters ‘AB’ and ‘CD’ at 90˚ (degree) angles to each other.

 

(iii) Now, draw the diameters ‘EF’ and ‘GH’ bisecting angles AOC and COB (angles, AOC = COB = 90˚).

 

(iv) Join ‘AE’, ‘EC’, ‘CH’, ‘HB’, ‘BF’, ‘FD’, ‘DG’, and ‘GA’ in straight lines and complete the required regular Octagon.

 

 

 

2. Three Circle Method

Draw a regular Pentagon (5 sides) with “3 Circle Method”:

 

Process:

(i) Draw a horizontal line ‘AB’ equal to the given length.

 

(ii) Take center as point ‘A’ and radius AB, and draw a circle-1.

 

(iii) Similarly, take center on point ‘B’ and with the same radius, describe a circle-2, cutting circle-1 at points ‘C’ and ‘D’ as shown in the image.

 

(iv) Now, take center on point ‘C’, and with the same radius, draw another circle-3, or an arc to cut circle-1 and circle-2 at points ‘E’ and ‘F’ respectively.

 

(v) With a compass, draw a perpendicular bisector on the line ‘AB’ to cut the circle-3 or the Arc ‘EF’ at point ‘G’. See figure.

 

(vi)Now, join ‘EG’ by a straight line and extend it to cut the circle-2 at point ‘P’.

 

(vii) Similarly, join ‘FG’ and extend it to cut the circle-1 at point ‘R’.

 

(viii) Now, take point ‘P’ and point ‘R’ as centers, and take the ‘AB’ as radius, draw two arcs intersecting each other at point ‘Q’.

 

(ix) Join ‘BP’, ‘PQ’, ‘QR’, and ‘RA’ in straight lines to complete the required regular pentagon.

 

 

 

 

3. Across Flat Method

 

Draw a regular Hexagon with the “Across Flat Method”:

Assume, the distance between two opposite parallel lines, or the distance across is 45 mm. See image.

 

Process:

(i) Draw a circle of diameter 45 mm (Radius = 45/2 = 22.5 mm).

 

(ii) Now, take the 30˚-60˚ set-square, and draw two horizontal parallel lines ‘BC’ and ‘FE’. See image.

 

(iii) With the same 30˚-60˚ set-square, draw opposite parallel lines ‘AB’ and ‘ED’, in such a way that it touches the circle tangentially and makes a 60˚ internal angle.

 

(iv) Similarly, again draw opposite parallel lines ‘CD’ and ‘FA’ in the same manner.

 

(v) Mark carefully the sides of the regular Hexagon with a Continuous-thickline to get the required Hexagon.

...[ Videos coming ]...