Spiral

 

Post Summarisation:

 

1. Spiral

2. Archimedean Spiral

3. Logarithmic Spiral

 

Spiral:

 

When a line rotates on a plane about one of its end, on such a way that a point moves along the line continuously in one direction (inward or outward), the curve traced out by the moving point is called a Spiral.

The point about which the curve line rotates is called a Pole.

 

The line joining any point on the curve with the pole is called the Radius Vector and the angle between this line and the line in its initial position (or, Horizontal axis line) is called the Vector angle or Vectorial angle.

 

Each complete revolution of the curve is termed the Convolution. A spiral may make any number of convolutions before reaching the pole.

 

 

Archimedean Spiral:

When a curve is traced out by a moving point in such a way that its movement inwards or outward from the pole is uniform with the decrease or increase of Vectorial angle, is called an Archimedean Spiral.

 

Uses: The use of this curve is made in teeth profiles of helical gears, profiles of cams etc.

 

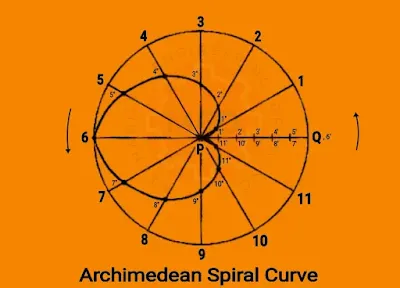
1. Problem: How construct an Archimedean spiral of 1⅟₂ convolutions, where given the greatest and the shortest radii are OP = 120 mm and OQ = 30 mm respectively.

 

Let, O is the pole.

 

(i) Draw a circle, taking point O as center and radius equal to OP = 120 mm. Mark point Q on OP, from O at a 30 mm distance (In this regards, you can draw another circle too with radius OQ and taking the center as O). Therefore, distance QP= (OP-OQ) = 90 mm.

 

(ii) Divide the Φ120 circle into 12 equal parts. So, each part or sector would be of 30˚. Naming them 1’, 2’, 3’, 4’, 5’, 6’, 7’, 8’, 9’, 10’, 11’, 12’.

(iii) For 1⅟₂ convolutions equal to (360˚+180˚) = 540˚. Now, 540˚/30˚ = 18. So, the distance QP = 90 mm need to divide into 18 equal divisions. Name them from P to Q (See the image) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, and 18. Hence, when the curve moves 30˚, means distance covered by the curve equal to one division of QP i.e. 5 mm.

 

(iv) Now, draw arcs with centre O and radius O1, and intersect the line O1' at point P1.

(v) Similarly, draw arcs with center O and radii O2, O3, O4, O5, O6, O7, O8, O9, O10, O11, O12, and intersect the lines O2’, O3’, O4’, O5’, O6’, O7’, O8’, O9’, O10’, O11’, and O12’ respectively at points P2, P3, P4, P5, P6, P7, P8, P9, P10, P11, and P12 respectively for one convolution.

 

(vi) Now, for another half convolution, draw arcs again with center O and radii O13, O14, O15, O16, O17, O18, and intersect the lines O13’, O14’, O15’, O16’, O17’, and O18’ respectively at points P13, P14, P15, P16, P17, and P18 respectively.

 

(vii) Atlast, join these points P, P1, P2, P3, P4, P5, P6, P7, P8, P9, P10, P11, P12, P13, P14, P15, P16, P17, and P18 by a smooth-thick curve line with the help of French curves or by Free hand to get the required Spiral Curve.

 

 

Tangent and Normal on Archimedean Spiral:

 

To draw a Tangent and normal on an Archimedean spiral at any point, first we need to find out the Constant of the Curve. The Constant of the Curve is equal to the difference between the lengths of two radii divided by the circular measure of the angle between them.

 

Mathematically,

 

Constant of Curve (C) =

(Major radius – Minor radius) / 2π × Number Of Convolution

=(120-30) / 2π × 1.5 mm           (As, π=22/7)

= 9.55 mm.

= 9.5 mm. (Approx)

Now, assume any point ‘N’ on the Archimedean Spiral where we need to draw a Tangent and Normal on the curve.

 

(i) Join N with the pole O to draw the radius vector NO.

 

(ii) Draw a perpendicular line OM equal in length to the Constant of the Curve = 9.5 mm, towords the decreasing side of the curve. See the image.

 

(iii) Now, join M with N by means of a straight line which is the normal to the spiral.

 

(iv) At last, draw a straight line ST, perpendicular to NM. This ST is the tangent of the Archimedean Spiral Curve on point N.

 

 

 

2. Problem: A pendulum 110 mm long hanging on a pivot O, swings from its vertical position of rest to the right through an angle of 75° and returns to its initial position at uniform velocity. During this period, a point P moving at uniform speed along the centre line of the pendulum from a point at a distance of 15 mm from O, reaches the end of the pendulum. Draw the locus of the point P.

 

(i) Draw a vertical line OA, 110 mm long.

(ii) With centre O and radius equal to OA, draw an arc.

(iii) Draw a line OB making ∠AOB equal to 75° and cutting the arc at B.

(iv) Mark a point P along OA and at a distance of 15 mm from O.

(v) Divide the angular movement of the pendulum and the line PA into the same number of equal parts, say 8. The end A of the link moves to B and returns to its original position.

Hence, the arc AB must be divided into four equal parts.

 

(vi) With centre O and radii O1, O2, O3, O4, O5, O6, and O7, draw arcs intersecting lines O1', O2', O3', OB, O5’, O6’,and O7’ respectively at points P1, P2, P3, P4, P5, P6, and P7 respectively.

(vii) Atlast, draw a curve through P, P1, P2, P3, P4, P5, P6, P7, and A. This Archimedean curve is the locus of the point P.

 

 

 

3. Problem: A straight link PQ of 60 mm length revolves one complete revolution with uniform motion in anti-clockwise direction about hinged P. During this period an insect moves along the link from P to Q and Q to P with uniform linear motion. Draw the path of the insect and name the curve.

 

(i) Draw circle of 60 mm radius at P as centre and divide into twelve equal parts. Name in anticlockwise direction 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, Q.

 

(ii) Divide line PQ into six equal part and mark as 1 ', 2', 3', 4', 5' and 6' and from Q as 7' to P.

(iii) Take the center as P and mark 1", 2", 3", 4", 5" and 6 along radius P1, P2, P3, P4, P5 and P6 respectively taking the radius with P1’, P2’, P3’, P4’, P5’, and P6’ respectively. As that insect gradually moves towards point Q and so, each division of the line PQ, as shown in image.

 

(iv) Now, as the insect moves at uniform speed, so the bottom portion would be the mirror image of top portion. So repeat the drop the respective point on bottom radii and name them as 7’’, 8’’, 9’’, 10’’, and 11’’.

 

(v) Atlast, join these points (starting from P, 1", 2", 3", 4", 5", 6, 7’’, 8’’, 9’’, 10’’, 11’’, and P) with the smooth-thick curve. This curve is the required Archimedean spiral.

 

 

 

Logarithmic Spiral or Equiangular Spiral:

 

When a spiral curve is traced out by a moving point in such a way that its distance from the pole is gradually increasing or decreasing, is called a Logarithmic Spiral.

 

In other words, when the radius vectors of a spiral are following Geometrical progression, is called a Logarithmic Spiral.

 

 

Arithmetic Progression (A.P): A succession (series) of numbers are in Arithmetic Progression (A.P), if difference between each term and its preceding term is a constant.

 

Let assume, a series of numbers = 1, 2, 3, 4, 5

In this series, 2-1 = 1

                         3-2 = 1

                         4-3 = 1

                         5-4 = 1

So, the difference between each term and its preceding term = 1 = Constant.

Therefore, we can say, this series of numbers are in Arithmetic Progression (A.P.).

 

Geometric Progression (G.P): A series of numbers is called a Geometric Progression (G.P.), if ratio(r) of each term in that series and its preceding term is a Constant. This ratio(r) is called Common ratio = Constant.

 

Now, let assume, a series of numbers = 2, 4, 8, 16, 32

In this series, 4/2 = 2

                         8/4 = 2

                        16/8 = 2

                        32/16 = 2

So, the ratio(r) of each term and its preceding term = 2 = Constant.

Therefore, we can say, this series of numbers are in Geometric Progression (G.P.).

 

In a logarithmic spiral, the ratio of the lengths of consecutive radius vectors enclosing equal angles is always constant. In other words the values of vectorial angles are in arithmetical progression and the corresponding values of radius vectors are in geometrical progression.

 

The logarithmic spiral is also known as Equiangular Spiral because of its property that the angle which the tangent at any point on the curve makes with the radius vector at that point is constant, thus this angle is termed as a Constant Angle.

 

 

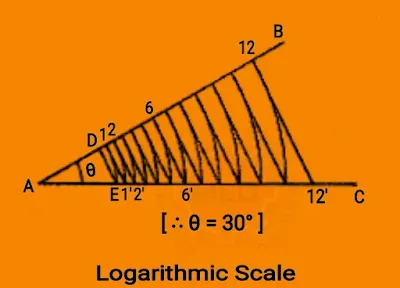
Problem: Construct a logarithmic spiral of one convolution, given the length of the shortest radius 1 cm long and the ratio of the lengths of radius vectors 10:9 enclosing an angle ϴ = 30˚. Also, draw a tangent and normal on any point on the spiral.

 

Solution:

 

Given, the shortest radius = 1 cm,

                                            ϴ = 30°

      And, Common ratio (r) = 10:9 = 10/9 ·

 

The lengths of radius vectors are determined from a scale which is called Logarithmic Scale. The Logarithmic Scale is constructed as shown below:

 

(i) Draw lines AB and AC making an angle of ϴ = 30° between them.

 

(ii) As, Common ratio = 10/9, so, on AC, mark a point E such that AE = 1 cm = 10 mm and on AB (for easy calculation), mark a point D such that AD = 9 mm. (or, if AD is taken as 1 cm long then AE would be 10/9 cm).

(iii) Draw a straight line to join D with E.

 

(iv) With centre A and radius AE, draw an arc cutting AB at a point 1. Through 1, draw a parallel line to DE and cutting AC at 1'. Again, with centre A and radius A1' draw an arc cutting AB at 2. Through 2, draw a parallel line to DE and cutting AC at 2'. Repeat the process and obtain points 3, 4, 5, 6, 7, 8 ,9, 10, 11, and 12 (as, angle between two consecutive vectors is ϴ = 30˚ and total number of vector radii required for 1 convolution = 360˚/30˚ = 12 numbers). As we know, number of Vector radii = No. of Convolution × 360˚/ϴ

 

So, this is the required Logarithmic Scale.

 

To draw a Logarithmic Spiral, first of all...

 

(i) Draw a horizontal line OQ and mark OP = AE (from the Logarithmic Scale) = 1 cm long.

 

(ii) Now, take OP line as a radial line and through O, draw 11 more radial lines making 30° angles between two consecutive lines.

 

(iii) Now, from Logarithmic Scale, take the lengths A1, A2, A3, A4, A5, A6, A7, A8, A9, A10, A11, A12 and mark on the radial lines as P1, P2, P3, P4, P5, P6, P7, P8, P9, P10, P11, and P12 respectively (See the image) to locate the spiral.

 

(iv) Join these points P, P1 , P2, P3, P4, P5, P6, P7, P8, P9, P10, P11, and P12 with a smooth-thick curve by means of free hand or by French cuves. This curve is the required logarithmic spiral.

 

Now, to draw the tangent and normal on the Spiral, we need to find out Constant Angle= α

 

As we know, tanα = 0.4343/log(r) × ϴ in radians   [r = common ratio = 10/9  and ϴ = 30˚]

 = 0.4343/log(10/9) × π/6 = 0.4343/0.0457 × 0.5235 = 4.9779

 ∴ α = tan-1(4.9779) = 78.63˚

 

(i) Assume any point, say N on the logarithmic curve.

 

(ii) Join point N with the pole O by means of a straight line.

 

(iii) Now draw an angle ∠TNO = α = 78.63˚ towords the decreasing side of the curve at point N, taking the base line as NO.

 

(iv) Extend the TN line to a suitable distance S. Now, this TS line is the tangent of that curve.

(v) Now, draw a perpendicular NR at point N (See image).

 

(vi) This NR is the normal of that tangent.