GEOMETRIC CONSTRUCTIONS (Part-A)

Geometric Constructions or Geometrical Constructions are mostly based on the basic simple geometry, though which is essential in the preparation of Engineering Drawings.

Without having better knowledge and practice in Geometric Construction, it is very difficult to complete any kind of Engineering Drawing.

The most commonly and generally used geometric constructions to construct any kind of engineering drawing are described below:

(1) To draw perpendiculars of a given line.

(2) To draw parallel lines.

(3) To bisect or equally divide a given line into two parts.

(4) To divide a line into any number of equal parts.

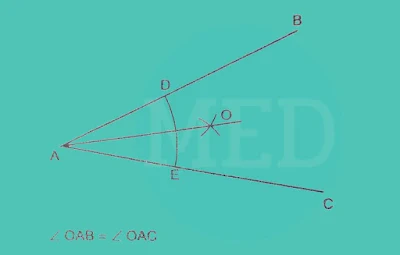
(5) To bisect (Divide into two equal parts) an angle.

(6) To divide a circle.

(7) To trisect (Divide into three equal parts) an angle.

(8) To draw an arc with a given radius.

(9) To draw tangent and normal.

(10) To draw a continuous curve.

(11) To construct an ogee or reverse curve.

(12) To draw a loop of three (3) circles pattern.

[For simplicity, we'll discuss No.1 to No.5 as 'Part-A' on this page and No.6 to No.12 as 'Part-B' on a different page.]

PART - A

(1) How to draw perpendiculars of a given line from a given point.

Drawing a perpendicular (90°) to a given line from a given point outside of the line can be obtained very easily with the help of either a protractor, set squares, or a compass.

However, here we shall discuss drawing perpendicular lines with the help of a compass only. Those methods are described as under:

(a) When the given point is out of the given line but nearer to the center than the end of the given line (see Fig.).

Let's consider a given line AB with any suitable length and C is the point.

(i) With center C and any convenient radius, draw an arc cutting the given line AB at E and F, respectively.

(ii) With any radius greater than half of EF and taken centers as E and F, draw the arcs intersecting with each other, on both sides of the given line at points C and G.

(iii) Draw a line joining C and G with a straight line.

Hence, CG is the required perpendicular line.

(b) When the given point is out of the given line but nearer to the end than the center of the given line (see Fig.).

Let's consider AB to be the given line and P the point.

(i) With center A and radius equal to AP, draw an arc PNP'.

(ii) With center N and radius equal to NP, draw an arc PMP'.

(iii) Draw a line joining P and P' and intersecting AB at F.

Then PP' is the required perpendicular on the given line.

(C) When the given point is anywhere on the given line (see fig.).

Let us consider, AB is a given line and P is the given point where we need to draw a perpendicular line.

(i) With P as the center and with any convenient radius, draw an arc that cuts AB at point C.

(ii) Now from point C, keeping the same radius, inscribe the arc into two equal divisions CD and DE respectively.

(iii) Again with the same radius and taking centres as D and E respectively, draw arcs intersecting each other at Q. Draw a straight line joining P and Q.

Then PQ is the required perpendicular line.

(D) When the given point is in the middle of the given line (see fig.).

(i) Let us consider AB as the given line. Taking a radius with a minimum half of AB and a maximum up to the length of AB, draw an arc from point A.

(ii) Similarly, taking center as B point and with the same radius draw another arc which cuts the previous arc at point O.

(iii) Now, join the middle point of the given line and point O with a straight line which is our required perpendicular.

Note: A perpendicular line that bisects or equally divides a straight line into two parts is called a Perpendicular Bisector of that straight line.

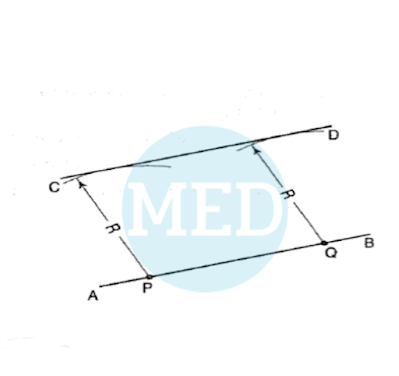
(2) How to draw a parallel line through a given distance or point and to a given straight line.

Let AB be the given line and a parallel line should be drawn at 25 mm apart from the AB line.

(i) Consider two separate points P and Q are on the AB line.

From point P and Q, draw two perpendiculars with the help of set-squares.

(ii) Now keeping P as the center, draw an arc with a 25 mm radius on CP (perpendicular line).

(iii) Similarly, taking the center as Q, draw an arc with a 25 mm radius, cutting the DQ perpendicular to point D.

(iv) Now join point C and point D by means of a straight line.

Then CD which is 25 mm distant from line AB and is the required parallel line of AB.

(3) How to bisect or equally divide a given line into two parts.

(i) Let's consider AB be the given line. With center A and radius greater than half of AB, draw arcs on both sides of AB (as shown in fig.).

(ii) Now, with center B and the same radius, draw arcs intersecting the earlier arcs at C and D, respectively.

(iii) Next, draw a line joining C and D and cutting AB at E.

Then AE = EB = ½ AB.

Furtherly, in the case of a curve line or arc, CD bisects AB arc at the right angle (see above fig.).

Let AB be the arc drawn with center O. Adopt the same above method as already described. The bisector CD will pass through the center O.

Watch this Vlog⤵️

(4) How to divide a line into any number of equal parts (say the length of a line is 65 mm and needs to be divided into 5 equal divisions). [Based on Thales Theorem]

Steps :

Draw a line AB to a convenient length ( suppose 65 mm).

(i) At point 'A' draw a line AC to a required length, such that will form an acute

angle BAC. (Always it is better to form an acute angle).

*An angle with less than a right angle (i.e. angle<90°), is called an Acute angle.*

(ii) Now, inscribe 5 equal arcs with the same radius continuously on the line AC, meeting at 1, 2, 3, 4 & 5. (As many equal parts as required. In this case, it is 5 numbers of equal divisions or parts)

(iii) Join points 5 & B with a continuous thin straight line.

(iv) From points 4, 3, 2 & 1 draw lines parallel to the '5B' line meeting the line 'AB' at 4', 3', 2' & 1' respectively with the help of sets square and pencil.

Now, the line AB is divided into 5 equal parts.

Watch this Vlog⤵️

(5) How to bisect a given angle.

Let's consider, angle BAC is the given angle.

(i) Now, keeping point 'A' as the center point, draw an arc with any convenient radius to cut the 'AB' and 'AC' lines at 'D' and 'E' respectively.

(ii) After this, taking a radius more than half of the linear length of 'DE' and point 'D' as the center, draw an small arc.

(iii) Similarly, with the same previous radius and taking point 'E' as the center, draw another arc that cuts the previous arc at point 'O'.

(iv) Join points 'A' and 'O' with a straight line.

(v) 'AO' is the bisector of the given angle BAC.

Therefore, angle OAB = angle OAC.

How to bisect Any Given Angle Or Trisect Any Given Angle, Using the Compass method?

Watch this Vlog⤵️

Geometric Constructions (Part-B) >>