Here, in this post, you'll read the rest topics from Geometric Constructions below...
(6) To divide a circle.
(7) To trisect (Divide into three equal parts) an angle.
(8) To draw an arc with a given radius.
(9) To draw tangent and normal.
(10) To draw continuous curve.
(11) To construct an ogee or reverse curve.
(12) To draw a loop of three (3) circles pattern.
Now we'll discuss them one by one...
(6) How to divide a circle into 8 or 12 numbers of equal sectors.
(i) A circle is divided into 8 numbers of equal sectors:
Let's consider a circle with any convenient radius.
As the total angle inside a circle is 360° and there are a total of 4 quadrants in a circle, so each quadrant should be of (360°/4 )= 90° (See figure below).
Now, the number of divisions should be equal to 8. So each sector should be of 45° (i.e. 360°/8=45°).
1. Draw a circle with any convenient length of radius and draw its axis lines AB & CD (See above image).
*Axis lines (one pair of imaginary lines) are always perpendicular (90°) to each other and pass through the center point of the object.*
2. Now keeping the same radius on your compass, start to bisect any two quadrants of the circle (for guidance, see how to bisect an angle).
In the above image, we've drawn arcs from point 'A' and point 'B' and cut those arcs from point 'C' with the same radius of circle on points 'E' and 'G' respectively.
Note: You can bisect each quadrant one by one but this will take more time.
3. There should be a total eight numbers of sectors inside the circle. So, join 'EO' and 'GO' respectively and extend those two bisectors 'EO' and 'GO' in a crosswise direction up to points 'F' and 'H' respectively till these would touch the circumference of the circle.
4. Now the given circle is divided into 8 numbers of equal sectors.
(ii) A circle is divided into 12 numbers of equal sectors:
The number of divisions should be equal to 12. So each sector should be of 30° (i.e. 360°/12=30°).
*Axis lines (one pair of imaginary lines) are always perpendicular (90°) to each other and pass through the center point of the object.*
5. Now, join the cut points in a crosswise direction with straight lines (as shown in the above image), and here, we have divided the circle into twelve(12) numbers of equal sectors.
How To Divide A Circle Into 8 Numbers Of Equal Parts Or Sectors, Using Compass?
(Watch Vlog ⤵️)
How To Divide A Circle Into 12 Numbers Of Equal Parts Or Sectors, Using Compass?
(Watch Vlog ⤵️)
How To Divide A Circle Into 3 Numbers Of Equal Parts Or Sectors, Using Compass?
(Watch Vlog ⤵️)
How To Divide A Circle Into 5 Numbers Of Equal Parts Or Sectors Using Compass?
(Watch Vlog ⤵️)
How To Divide A Circle Into 8 and 12 Numbers Of Equal Parts Or Sectors Using By Sets-Square?
(Watch Vlog ⤵️)
(7) How To Trisect A Given Angle:
(i) Trisect a Right Angle (90°):
Steps:
1. Draw a right angle (90°).
2. Taking point 'B' as a center, draw an arc with any convenient radius, meeting the line 'BA' and line 'BC' at point '2' and point '1' respectively.
3. Now, taking point '1' as a center and 'B-1' as the radius, draw an arc that cuts the previous '2-1' arc at point 'D'.
4. Similarly, taking point '2' as a center and 'B-2' as the radius, draw an arc that cuts the previous '2-1' arc at point 'E'.
5. Now, join 'BE' and 'BD' respectively with straight lines (as shown in the above image).
This is how we can trisect any right angle very easily.
Therefore,
Angle ABD = Angle DBE = Angle EBC
(ii) Trisect Any Given Angle:
Steps:
1. Let, angle ABC be the given angle.
2. Taking point 'B' as a center, draw an arc 'DE' with any convenient radius.
3. Joint 'DE' with a straight line (as shown in the above image).
4. Now, bisect the given angle ABC and draw the bisector 'BO' which cuts the line 'DE' at point 'F'.
5. Next, taking point 'F' as center and 'DF' as radius, draw a semicircle (as shown in the above figure).
6. Now, taking the same radius 'DF' on your compass, start to inscribe the periphery of the semicircle on point 'H' and on point 'G' respectively. Start to inscribe either from point 'E' or from point 'D' (as shown in the above image).
7. Next, join 'BG' with a straight line and extend it up to point 'I'. Similarly, join 'BH' and extend it up to point 'J'.
Now, we have divided that given angle ABC into three (3) equal divisions.
Therefore,
Angle ABI = Angle IBJ = Angle JBC.
How To Divide An Angle Into 2 Number Of Equal Parts And 3 Number of Equal Parts, Using Compass?
(Watch Vlog ⤵️)
(8) To draw an arc with a given radius:
Here, we will draw an arc of a given radius (say, r=25 mm), touching two straight lines at right angles.
Steps:
● Draw the lines 'AB' and 'AC' at right angles (See above image).
● Taking point 'A' as a center and given radius (r 25 mm), draw arcs to cut lines 'AB' and 'AC' at points 'E' and 'F' respectively.
● With points 'E' and 'F' as centers and the given radius (r 25 mm), draw arcs to intersect each other at point 'O' (as shown in the above image).
● Now, taking point 'O' as a center and with the same given radius (r 25 mm.), draw a curve that will just touch the lines 'AB' and 'AC'.
Now, we will draw an arc with a given radius (say r=25 mm.), touching two straight lines at any angle rather than a right angle (say at 60° angle).
Steps:
● Draw an angle BAC at 60°.
● Draw a horizontal parallel line 'EF' and an angular parallel line 'GH' respectively at a distance of a given radius (r 25 mm) in such a way that both drawn parallel lines would intersect each other at point 'O' (as shown in the above figure).
● Taking point 'O' as a center and with the given radius (r 25 mm), draw a curve touching both lines 'AB' and 'AC'.
These are how we can draw a curve or arc with a given radius.
(9) How to draw tangent and normal:
A straight line, just touching a given curve on a specific point and perpendicular to the Normal at the point of contact on the given curve, is called a Tangent.
A Normal is a line perpendicular to the Tangent at that point of contact on the curve.
The point of contact of Tangent and Normal on the curve is also termed as Point of Tangency.
Steps:
• In common cases for a circle, the Point of Tangency is given or assumed at any point on the circumference of the circle.
• Now, join that point and the center of the circle using a straight line that would be the Normal.
• Lastly, draw a straight line on that specific point on the circumference and perpendicular to the Normal. This straight line would be the Tangent of the circle.
Later in a different post, we'll see in more details, the methods to draw tangents and normal on different types of curves i.e. on circles, ellipses, parabolas, etc.
(10) How to draw a Continuous Curve:
In simple words, a Continuous Curve means a combination of any number (more than one!) of smooth curve lines without making any corners or cross or cut points.
Practically, a railway track is one of the best examples of a Continuous Curve.
To draw a continuous curve in the following geometrical method, we require a minimum of three (3) points of any distance.
Here, we will draw a continuous curve with five (5) points. See given picture below.
However, we can assume even more points to draw a continuous curve.
Steps:
Let's assume A, B, C, D, and E are the given points and randomly mark these points on the drawing sheet (See the above image).
1. Now, draw straight lines by joining point A with point B, point B with point C, C with D, D with E, and so on! (This kind of line is also termed a Poly-line.)*
2. Draw perpendicular bisectors ( ① & ② ) on 'AB' and 'BC' respectively, intersecting at point 'J'.
3. Now, taking point 'J' as the center and radius equal to 'JA', draw an arc ABC.
4. Draw the perpendicular bisector ( i.e. ③ ) on CD.
5. Now, join 'JC' with a straight line, and extend up to a limit that 'JC' would cut the perpendicular bisector ( i.e. ③ ) of line 'CD' at point K.
6. Take point K as the center and radius equal to KC, and draw an arc CD.
7. Now draw again, the perpendicular bisector ( i.e. ④ ) of DE.
8. This time, join 'KD' with a straight line, and extend up to a limit that 'KD' would cut the perpendicular bisector ( i.e. ④ ) of line 'DE' at point L.
9. Take point L as the center and radius equal to LD, and draw an arc DE as shown in the above image.
Now, ABCDE is our required continuous curve drawn with five (5) random points.
Note:
(i) The center point of every arc is at the
the intersection of the perpendicular bisector and the line produced by joining the previous center point with the last point of the previous arc.
(ii) The curve should be continuous. So, no corner should be produced on it.
(iii) At the very end, make the continuous curve thick and dark very carefully to provide better visual effects.
(11) How to construct an ogee or reverse curve:
An Ogee or a Reverse curve consists of two similar curves in which one curve has a reverse shape to the other curve. In other words, any curve corresponds to a continuous double curve with one part convex and the other part concave, it's said to be an Ogee or Reverse Curve. See the below image...
Steps:
1. To draw an Ogee, first of all, we need to draw two straight parallel lines in such a manner that the 'end point' of one line rests apart from the 'starting point' of the other line. See the 'AB' and 'EF' lines in the above picture.
2. Let 'AB' and 'EF' be the two assuming or given parallel lines that would be connected by an Ogee.
3. Now, join points B and E with a straight line.
4. Bisect the line 'BE' and mark its center point at T.
5. Bisect line segment 'BT' and draw the bisector line 'PQ'.
Similarly, bisect segment 'ET' and draw the bisector line 'RS'.
Similarly, bisect segment 'ET' and draw the bisector line 'RS'.
6. From point B, draw a perpendicular line to cut the bisector line 'PQ' at C.
Similarly, from point E, draw a perpendicular line to cut the bisector line
'RS' at D.
Similarly, from point E, draw a perpendicular line to cut the bisector line
'RS' at D.
Points C and D would be the center points of the required Ogee or Reverse curve.
7. Now, take point C as the center and BC as the radius, and draw an arc BT.
Similarly, keep point D as the center and DE as the radius, and draw another arc ET.
Now, curve BTE is the required Ogee or Reverse curve.
Similarly, keep point D as the center and DE as the radius, and draw another arc ET.
Now, curve BTE is the required Ogee or Reverse curve.
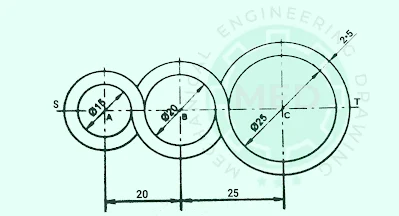
(12) How to draw a loop of three (3) circles:
There are many patterns of loops with three (3) circles. However, the following loop of the three circles pattern is mostly used in practical workshops.
Steps:
1. Draw any straight line ST of 70 mm. length. See the above image.
2. Mark points A, B, and C on the line so that SA = 10 mm, AB = 20 mm, BC = 25 mm and CT = 15 mm.
3. Take point A as a center and draw concentric circles of dia 15 mm (radius 7.5 mm) and dia 20 mm (radius 10 mm), see above image.
4. Now, take point B as the center and draw concentric circles of dia 20 mm (radius 10 mm) and dia 25 mm (radius 12.5 mm), see the above image.
5. Again draw concentric circles with a dia 25 mm (radius of 12.5 mm) and a dia 30 mm (radius of 15 mm), taking point C as the center.
6. Erase unnecessary parts, thick and darken the lines to make the pattern form as shown in the above fig.













-Points.jpg)