INVOLUTE

 

Post Summarisation:

 

1. Definition of Involute

2. Use of Involute

3. Involute of a Circle

4. Involute of a Triangle

5. Involute of a Square

6. Involute of a Pentagon

5. Involute of a Semi Circle

6. Involute of a Pole

7. Tangent and Normal on an Involute

 

1. Definition: What is an Involute?

When a curve traced by the end point on a straight line which rolls out without any slipping along from a circle or a polygon, such curve is called as an Involute.

For simplicity, it is a curve generated by an end of a piece of thread, from roll tight around a circle or a polygon to unwound condition.

Mathematically, it can be described by x = rcos8 + r8sin8, y = rsin8 - r8cos8, where, "r" is the radius of a circle.

 

2. Use of Involute:

Practically, Involutes are generally used in drawing of Belt Drive, Chain Drive, Teeth Profile of a Gear, etc.

 

3. How to Draw an Involute of a Given Circle?

Construction:

(i) Draw a Circle of given radius.

(ii) Divide the circle into twelve (12) equal parts or sectors.

(iii) Assume the base point of the circle is ‘P’, and starting from P, mark each part on the circumference at clockwise direction as 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11. (See the image)

(iv) Now, draw a horizontal line from the point P, tangentially to the circle and equal to the circumference of the circle, give a name PQ to the line.

(v) Divide the line PQ into 12 equal divisions and mark each division as 1’, 2’, 3’, 4’, 5’, 6’, 7’, 8’, 9’, 10’, and 11’. (See the image)

 (vi) Now, take the length of P-11’ on compass, and draw a tangent on the circle at point 11, equal to the length of P-11’.

(vii) Similarly, take the length of P-10’, P-9’, P-8’, P-7’, P-6’, P-5’, P-4’, P-3’, P-2’, P-1’ and draw tangents equal to those lengths at points 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 respectively.

(viii) Give the name to the tangents accordingly as P11-11, P10-10, P9-9, P8-8, P7-7, P6-6, P5-5, P4-4, P3-3, P2-2, P1-1. (See the image)

(ix) Now, draw the Involute through these points P, P1, P2, P3, P4, P5, P6, P7, P8, P9, P10, P11, and Q with the help of French curves.

 

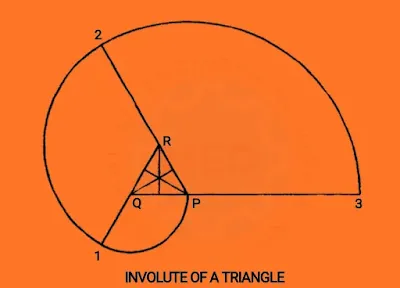
4. How to draw an Involute of a given Triangle (Applicable for Any Triangle)?

Construction:

(i) Draw a triangle PQR with any given length of sides. Assume, the length of sides are PQ, QR, and RP.

(ii) Extend all three lines on same manner. (See Image, Extended lines should not start from a common point.)

(iii) Consider starting point P. You can assume any point as a starting point only by the error free calculation.

(iv) Now, moving clockwise direction, take point Q as centre, and PQ as radius, cut an arc on the extended part of line QR. Name the cut as ‘1’.

(v) Again, take point R as center, and take radius = (PQ+QR), cut an arc on the extended part of line PR. Give it a name as ‘2’.

(vi) Now, take point P as center, and take radius = (PQ+QR+RP), intersect on the extended part of line QP. Name the intersect point as ‘3’.

(vii) Atlast, draw the curve with French Curves through these points 1, 2, and 3 to get the required Involute.

This method is applicable for any Triangle ,or  polygon with any length of sides.

 

 

4. How to draw an Involute of a given Square (Applicable for Any Square)?

Construction:

(i) Draw a Square PQRS with any given length of sides. Assume, the length of sides are PQ, QR, RS, and SP.

(ii) Extend all four lines on same manner. (See Image, Extended lines should not start through a common point.)

(iii) Consider starting point S. You can assume any point as a starting point only by the error free calculation.

(iv) Now, moving clockwise direction, take point P as centre, and SP as radius, cut an arc on the extended part of line PQ. Name the cut as ‘1’.

(v) Again, take point Q as center, and take radius = (SP+PQ), cut an arc on the extended part of line QR. Give it a name as ‘2’.

(vi) Now, take point R as center, and take radius = (SP+PQ+QR), intersect on the extended part of line RS. Name the intersect point as ‘3’.

(vii) Similarly, take point S as center, and take radius = (SP+PQ+QR+RS), intersect on the extended part of line PS. Name the intersection point as ‘4’.

(viii) Atlast, draw the curve with the help of French Curves through these points 1, 2, 3, and 4 to get the required Involute.

 

 

5. How to draw an Involute of a given Pentagon (Applicable for Any Polygon)?

Construction:

(i) Construct pentagon of sides with given length.

(ii) Name the corners (Apex) of Pentagon as P, Q, R, S, and T as shown in the image.

(iii) Extend all five lines such that none of them start from a common point. See the mage.

(iv) Assume starting point T. You can assume any point as a starting point only by the error free calculation.

(v) Now, moving clockwise direction, take point P as centre, and PT as radius, cut an arc on the extended part of line PQ. Name the cut as ‘1’.

(vi) Again, take point Q as center, and take radius = (PT+PQ), cut an arc on the extended part of line QR. Give it a name as ‘2’.

(vii) Now, take point R as center, and take radius = (PT+PQ+QR), intersect on the extended part of line RS. Name the intersect point as ‘3’.

(viii) Similarly, take point S as center, and take radius = (PT+PQ+QR+RS), intersect on the extended part of line PS. Name the intersection point as ‘4’.

(ix) Again, take point T as center, and take radius = (PT+PQ+QR+RS+ST), cut an arc on the extended part of line PT. Give it a name as ‘5’.

(x) Atlast, draw the curve with the help of French Curves through these points 1, 2, 3, 4 and 5 to get the required Involute of an Pentagon.

 

 

6. How to draw an Involute of a semi-circle?

 

A thin semi-circular plate of radius 32 mm is fixed. A rope of 140 mm length, which one end is fixed and 20 mm below and 20 mm on the right from center of that plate. The rope is wound in anti-clockwise direction around the circumference of the plate. Draw the locus of free end of the rope.

Construction:

(i) First, draw the semicircle of radius 32 mm and mark the center point as C.

(ii) Mark point ‘O’ from 20 mm below and 20 mm on the right of C.

(iii) Now, draw OP of 140 mm length, parallel to the diameter of the semi-circle.

(iv) Divide the semi-circle into six equal parts and label it 1, 2, 3, 4, 5, 6 and 7. Join all points with C.

(v) Now, rotate anti-clockwise the line OP about O (assume point O is fixed), till it touches the semicircular plate at point 1. Mark the point 1 as point 1' on the rope.

(vi) Mark 7' on line 1'P0 from 1' such that 1'7' = πR = 100.48 mm (Periphery of the semi-circle). Divide 1 '-7' into six equal parts and name it as 2', 3', 4', 5', and 6’.

(vii) Now, draw tangents on semicircular plate at 1, 2, 3, 4, 5, 6 and 7 in anticlockwise direction such that 1-P1 = 1 '8', 2-P2 = 2'8', 3-P3 = 3'8', 4-P4 = 4'8', 5-P5 = 5'8', 6-P6 = 6’8’, and 7-P7 = 7'8' respectively.

(viii) Atlast, join points P, P0, P1, P2, P3, P4, P5, P6, and P7 by smooth thick curve line to get the required Involute.

The image shows the curve traced out by the free end of that rope which is longer than the circumference of the semi-circle on which it is wound.

 

7. A straight line AP is 100 mm long, trace it’s path when it rolls, without slipping, on a semi-circle having diameter AB, 75 mm.

Construction:

(i) Draw the semi-circle of diameter 75 mm, and divide it into six equal parts.

(ii) Assume, the line AP to be tangent to the semi-circle in starting position. Draw the line AP and mark points 1, 2, 3, 4, and 5. such that A1 = arc A1 ', A2 = arc A2', A3 = arc A3’, A4 = arc A4’, and A5 = arc A5’. The last division 5P will be of a shorter length.

(iii) On the semi-circle, mark a point P' such that 5P = 5’P’.

(iv) Now, draw tangents on points 1’, 2’, 3’, 4’, and 5’,

(v) Mark points P1, P2, P3, P4, and P5 on tangents such that 1' P1 = 1P, 2' P2 = 2P, 3’ P3 = 3P, 4’ P4 = 4P. and 5' P5 = 5P.

(vi) Similarly, mark points A1, A2, A3, A4, A5 on tangents such that 1’A1 = 1A, 2'A2 = 2A, 3’A3 = 3A, 4’A4 = 4A, and 5’A5 = 5A, and P’A'= PA.

(vii) Draw the required curve through points P, P1, P2, P3, P4, and P5 or P’, when the straight line is elastic and rolls round to the semi-circle. And through points A, A1, A2, A3, A4, A5 and A'. If the straight line is inelastic. Ultimately, both curves are tracing the complete path of that straight line.

The one end is A, attached to the semicircle, the other end P will trace out by the curve PP' when the straight line is rolls round on the semi-circle.

 

 

8. How to draw an Involute of a Pole?

AP is a rope 1.50 metre long, tied to peg at A (as shown in the given image), keeping it always tight, the rope is wound round the pole. Draw the curve traced out by the end P. Use scale 1:20.

Construction:

(i) Draw the given figure as per the scale.

(ii) From A, draw a line passing through 1. A as centre and AP as radius, draw the arc intersecting extended line A1' at P0. Extend the side 1-2, 1 as centre and 1 'Po as radius, draw the arc to intersect extended line 1-2 at P1.

(iii) Divide the periphery of the semi-circle into six equal parts and label it as 2, 3, 4, 5, 6, 7, and 8.

(iv) Draw a tangent to semicircle from 2 such that 2'-P1 = 2'-P2 . Mark 8' on this tangent such that 2'-8' = πR (Periphery or Circumference of Semi-Circle). Divide 2'-8' into six equal parts.

(v) Similarly draw tangents at 3, 4, 5, 6, 7 and 8 in anti-clockwise direction such that 3-P3 = 3'-9', 4-P4 = 4'-9', 5-P5 = 5'-9', 6-P6 = 6'-9', 7-P7 = 7'-9', 8-P8 = 8'-9' and 8-P9 = 8'-9' respectively.

(vi) Join P, P0, P1, P2, P3, P4, P5, P6, P7, P8, and P9 with smooth thick curve to get the required Involute.

 

 

 

 

9. How to draw a tangent and normal on the Involute of a circle at a point N on it?

Construction:

(i) Draw a line joining C with N.

(ii) With CN as diameter describe a semi-circle cutting the circle at M.

(iii) Draw a line through N and M. This line is the Normal. Draw a line ST, perpendicular to NM and passing through N. ST is the tangent on the Involute.

The normal to an Involute of a circle is tangent to that circle.